Polynomial Distortion Example

Adapted example from ImageMagick docs.

Use control points from file grid16-control-points.txt to distort source image:

Example code:

import {
  distortUnwrap,
  toHTMLCanvasElement,
  Canvas,
  VirtualPixelMethod,
} from "@alxcube/lens";

// load and parse control points file
const response = await fetch("./grid16-control-points.txt");
const controlPoints = (await response.text()).trim().split(/\s+/m).map(Number);

// load source image
const image = await Canvas.createFromUrl("./grid16.png");

// distortion arguments
const polynomialOrder = 3;
const distortionArgs = [polynomialOrder].concat(controlPoints);

// distort image
const distorted = await distortUnwrap(image, "Polynomial", distortionArgs, {
  virtualPixelMethod: VirtualPixelMethod.GRAY,
});

// display result
document.body.appendChild(toHTMLCanvasElement(distorted));

// invert mappings
const invertedControlPoints = [];
for (let i = 0; i < controlPoints.length; i += 4) {
  const [u, v, x, y] = controlPoints.slice(i, i + 4);
  invertedControlPoints.push(x, y, u, v);
}

// reverse distortion
const revertedImage = await distortUnwrap(
  distorted,
  "Polynomial",
  [polynomialOrder].concat(invertedControlPoints),
  {
    virtualPixelMethod: VirtualPixelMethod.GRAY,
  }
);

// display result
document.body.appendChild(toHTMLCanvasElement(revertedImage));

After applying first distortion, we get following result:

And after inverting control point mappings and distorting previous result, we get following image:

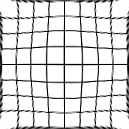
This shows that while a polynomial distortion works, and works well, it is not an exact or reversible distortion. Essentially the 81 coordinates are 'averaged' together so as to generate a mathematical 'best-fit' of the input coordinates.

Because more control-points (81) have been provided rather than the minimum (10) needed, none of the control points are guaranteed to exactly match the coordinates requested. However for this specific example, where the coordinaites are close to the expected distorted result, it should be reasonably close.

The polynomial function will generally have the most errors along the edges and especially in the corners of the image. This not only effects the pixel locations but also the sampling area (EWA) at the edges.

This is a natural result of the approximation used. A higher order polynomial could have been used, but in this case it does not make any great improvements. For this specific case, the polynomial is actually trying to fit itself to a non-polynomial trigonometric function. Due to the nature of those functions, the second distort will be more inaccurate than the first.